你将获得一个由n个顶点和m个边组成的无向图。你的任务是查找有几个连通分量是环。
以下是图论的一些定义。
1:无向图由两部分组成:一部分是节点(称为顶点)另一部分是边。每条边连接一对顶点。所有边都是双向的(如果顶点a与顶点b连接,则顶点b也与顶点a连接)。边不能将顶点与自身连接,且一对顶点之间至多有一条边。
2:任何连通图的连通分量只有一个,即是其自身,非连通的无向图有多个连通分量。
3:顶点u,v属于同一连通分量,当且仅当u和v之间至少含有一条边。
4:称为环的连通分量满足:
第一个顶点通过边连接第二个顶点,
第二个顶点通过边连接第三个顶点,
...
最后一个顶点通过边连接第一个顶点,
除上述描述的边外,没有其他的边,此时的连通分量被称为环
根据定义,每个环都含有三个或以上的定点。
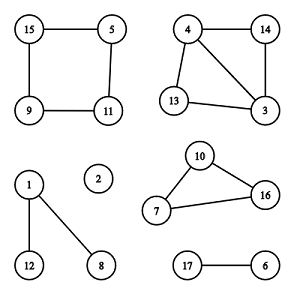
这是一张无向图,包含6个连通分量,其中2个为环,分别为[7,10,16]和[5,11,9,15]