懒散的水明准备去躺在草地上休息（草地可以看成由n*n个小格子组成的正方形），已知水明的大小为1*k，即占据连续的k个格子。但是他不知道他该占据哪些格子睡觉，他只知道哪些格子有石头，所以是不能睡的，因为不舒服。

所以请你们找到，那个最舒服的格子，即水明能竖躺、横躺（只要身体在格子上）方式最多的格子。

只要占据的所有格子中，有一个格子不一样即算两种方法。

第一行输入两个整数n和k（1≤k≤n≤100） - 草地的大小和水明的高度。

接下来的n行每行包含n个字符，每个字符都是'＃'（表示有石子的格子）或'.' （表示可躺的格子）。

输出两个整数 – 格子的行数和列数（左上角为1 1），属于水明能用不同方法躺下的最大数量的位置。

如果有多个答案，请输出优先级最高的，例如答案为x y，y越小优先级越高，若y相等，则x越小优先级越高。

样例：

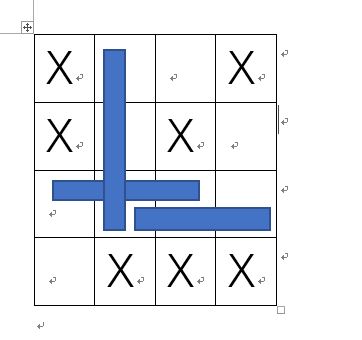
所以答案为3 2

p.s.普及模拟赛2018-4-C

Reach-Top