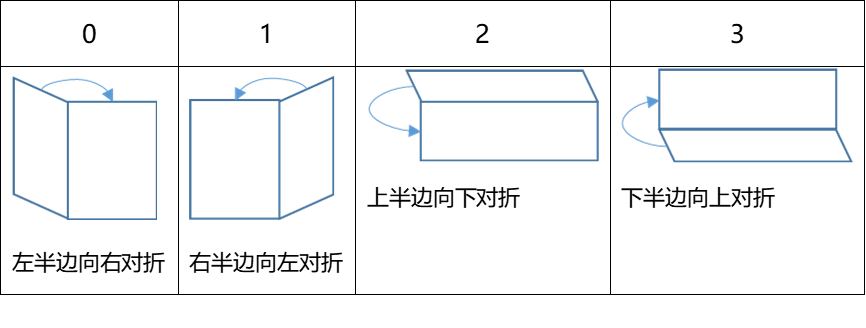
定义以下四种对折方式:
一张纸在左右对折n次,上下对折m次后,其表面的折痕将其分为(2^n * 2^m)个区域,对各区域进行如下方式编号:

现假设对折时纸不移动,若要求一张纸对折后落在区域(x, y)内,有多少种对折的顺序?
代码:
#include <iostream>
using namespace std;
int l, r, bottom, top; //区域边界
int n, m, x, y; //输入
int cnt = 0; //计数
char path[20] = "";
bool check()
{
return (l <= x && x < r && __(1)__);
}
int pow2(int exp)
{
int res = 1;
while (exp--)
res *= 2;
return res;
}
void dfs(int depth)
{
if (l == x && r - 1 == x && bottom == y && top - 1 == y)
{
__(2)__;
cout << path << endl;
}
else
{
int t;
if (r - l > 1)
{
//左半边向右折
t = l;
l = l + (r - l) / 2;
if (check())
{
__(3)__;
dfs(depth + 1);
}
l = t;
//右半边向左折
t = r;
__(4)__;
if (check())
{
path[depth] = '1';
dfs(depth + 1);
}
r = t;
}
if (top - bottom > 1)
{
//下半部分向上折
t = bottom;
bottom = bottom + (top - bottom) / 2;
if (check())
{
path[depth] = '2';
dfs(depth + 1);
}
bottom = t;
//上半部分向下折
t = top;
top = top - (top - bottom) / 2;
if (check())
{
path[depth] = '3';
dfs(depth + 1);
}
top = t;
}
}
}
int main()
{
cin >> n >> m;
cin >> x >> y;
l = 0;
r = pow2(n);
bottom = 0;
top = pow2(m);
dfs(0);
__(5)__;
return 0;
}