他们说“岁月就像多米诺骨牌，一个接一个地倒下”。但是，光阴的流逝能用骨牌来形容吗？我不这么认为。
一锐是个小机灵鬼。他最近得到了一个带有h行和w列的矩阵。每个单元格都是一个正方形，可以是空的（用'.'表示），也可以是非空的（用'#'表示）。行从上到下编号为 1 到 h。列从左到右编号为 1 到 w。
此外，一锐只有一张多米诺骨牌。他想把它放在矩阵的某个地方。多米诺骨牌将正好占据两个相邻的单元格，分别位于一行或一列中。两个相邻的单元格都必须为空，并且必须位于网格内。
一锐想再找点乐子，因此他决定搞些事情。在每次查询中，他都会选择一些矩形，并想知道有多少种方法可以将单个多米诺骨牌放入所选矩形内。
输入的第一行包含两个整数 h 和 w（1 ≤ h，w ≤ 500）–分别为行数和列数。
接下来的 h 行描述一个矩阵。每行包含一个长度为 w 的字符串。每个字符都是“.”或“#” — 分别表示空单元格或非空单元格。
下一行包含单个整数 q（1 ≤ q ≤ 100 000）— 查询次数。
接下来的q行每一行都包含四个整数r1i, c1i, r2i, c2i (1 ≤ r1i ≤ r2i ≤ h, 1 ≤ c1i ≤ c2i ≤ w) — 第 i 次查询。数字r1i和c1i分别表示矩形左上角单元格的行标和列标。数字r2i 和 c2i分别表示矩形右下角单元格的行标和列标。
打印 q 个整数，输出将单个多米诺骨牌放入第 i 个矩形内的方法数。
样例1输入 5 8 ....#..# .#...... ##.#.... ##..#.## ........ 4 1 1 2 3 4 1 4 1 1 2 4 5 2 5 5 8 样例2输入 7 39 ....................................... .###..###..#..###.....###..###..#..###. ...#..#.#..#..#.........#..#.#..#..#... .###..#.#..#..###.....###..#.#..#..###. .#....#.#..#....#.....#....#.#..#..#.#. .###..###..#..###.....###..###..#..###. ....................................... 6 1 1 3 20 2 10 6 30 2 10 7 30 2 2 7 7 1 7 7 7 1 8 7 8
样例1输出 4 0 10 15 样例2输出 53 89 120 23 0 2
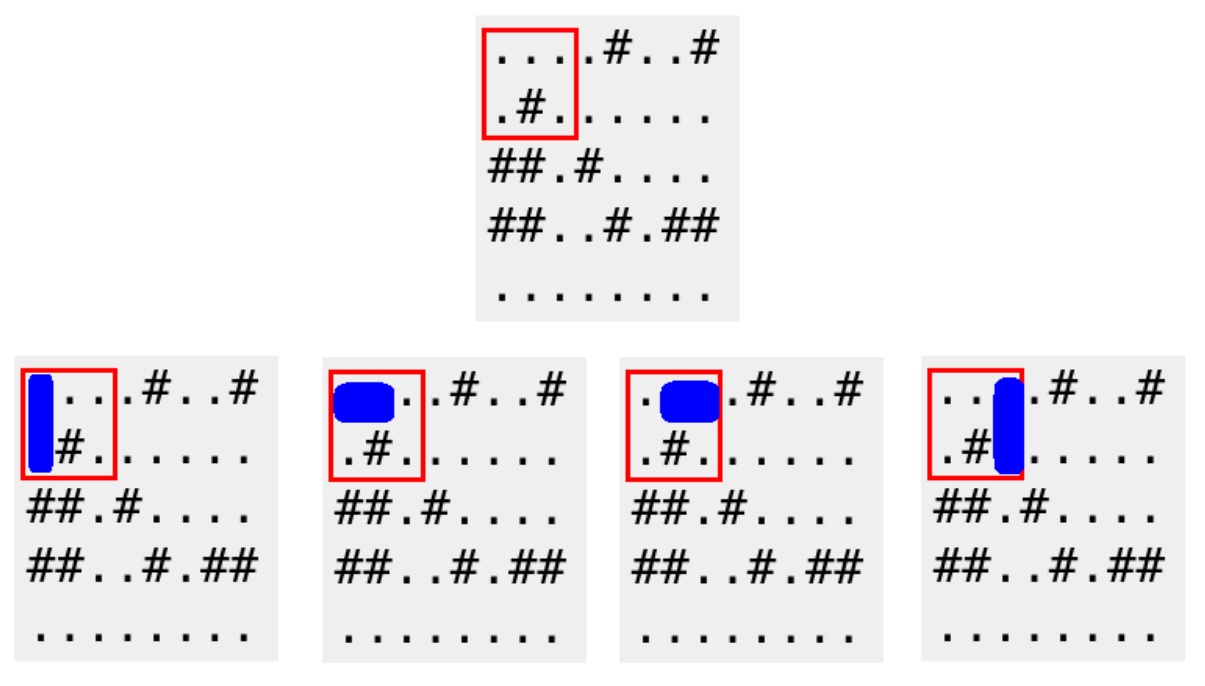
下面的红色框对应于第一个示例的第一个查询。多米诺骨牌可以以4种可能的方式放置。
