有 k 个选手在一棵 n 个节点的树上激情跑图，其中混入了一些具有“膜法”的强力选手。

具体的，树是一棵以 1 为根的叶向树（外向树），正常的选手只能沿着树边单向移动，而具有“膜法”的选手则可以任意穿梭。

你现在得到了 m 天内每天每个节点上有多少个选手，求最多有多少个没有“膜法”选手才能使记录合法。

第一行三个正整数 n,k,m ，分别表示树的节点个数、选手个数，以及记录天数。

之后的 n-1 行每行两个正整数 u,v ，表示有一条 u→v 的有向树边，保证 u<v 。

之后的 m 行每行 n 个非负整数，第 i 行的第 j 个数字记为 c[i][j] ，表示第 i 天编号为 j 的节点上有多少个选手。

数据保证对于任意 i∈[1,m] ，满足 \sum_{j=1}^n c[i][j]=k 。

一个正整数 x ，表示至多有 x 个选手没有“膜法”记录才会合法。

6 4 3
1 2
3 6
2 5
3 4
1 3
2 1 0 0 0 1
1 3 0 0 0 0
1 1 0 1 0 1

2

样例解释

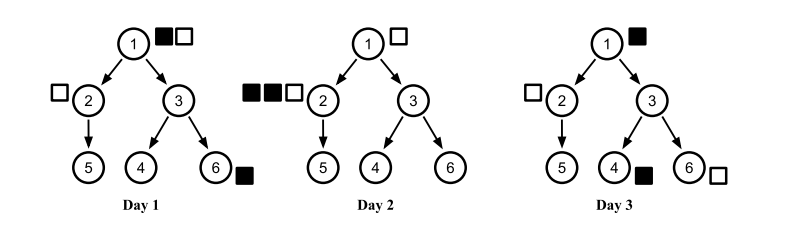
其中黑色格子表示具有“膜法”的选手，白色格子表示普通选手。
可以发现普通选手每天都只沿着树边走若干步，而“膜法”选手则无规则的任意穿梭。
不难发现没有减少黑色格子的方法，所以答案就是 2 。

数据规模
对于 100% 的数据，n≤1000,m≤200,k≤2×10^9 。

- subtask1（10 分）：n,m,k≤10 。
- subtask2（20 分）：对于 n-1 条树边 (u,v) ，保证均有 v=u +1 。
- subtask3（20 分）：m≤2。
- subtask4（50 分）：无特殊限制。