小 L 最近喜欢上了自动机算法，他认为这种优雅而高效的算法才是 OI 的本质。

给定一个 n 个节点，m 条边的有限状态自动机，1 为初始节点，有 p 个终止节点，转移只有大小写字母。

更通俗的，给定一个有向图，每条边上有一个字母，每个点出边上的字母不重复。

如果从初始节点 1 出发，对于给定字符串 s，按照上面的字符按顺序走对应出边，如果每次都有边可走，且最终走到了某个终止节点，那么称字符串 s 被该自动机接受。

例如对于样例 1 的自动机：



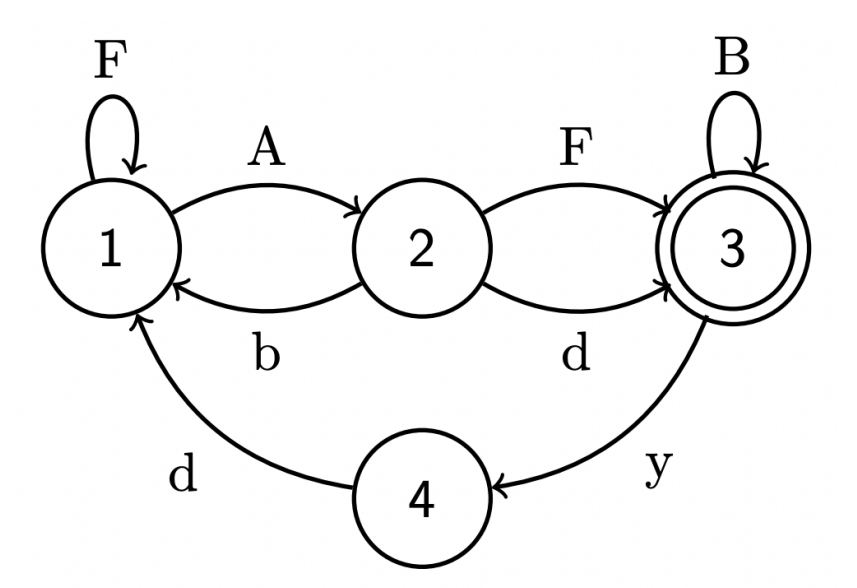
其中仅有 3 为终止节点。

那么 `FAFB` 或 `FAbFAbAd` 都是被接受的，而 `FF` 或 `FAc` 则不被接受。

求构造两个自动机可接受的串 a,b，使得 a,b 在去掉小写字母后完全相同，但是 a,b 本身不同。

注意，允许在删去小写字母后，a,b 均为空串，也允许 a,b 本身就是空串（前提当然是 a,b 能被自动机接受）。

小 L 并不关心具体的构造方案，他只需要你输出最小的 |a|+|b| ，如果无法构造，输出 `-1`。

第一行三个正整数 n,p,m 分别表示自动机的节点个数、自动机的终止节点个数，以及自动机的边数。

第二行  p 个正整数表示 p 个终止节点的编号，保证节点编号互不相同。

之后 m 行，每行形如 `u c v`，其中 u,v 为两个正整数，c 为一个小写或大写字母，表示一条 u→v 且边权为 c 的转移。

保证对于同一个 u，一种字母 c 至多出现一次。

一个正整数 x，表示最小的 |a|+|b| 。

样例1：
4 1 8
3
1 F 1
1 A 2
2 b 1
2 F 3
2 d 3
3 B 3
3 y 4
4 d 1

样例2：
2 2 1
1
2
1 a 2

样例3：
1 1 1
1
1 A 1

样例1：
10

样例2：
1

样例3：
-1

样例解释
样例 1 图可以看题面。

发现 `AdydAF` 和 `AbAF` 两个串是一组合法解，且可以证明没有更小的 |a|+|b|。

样例 2，发现 空串 和 `a` 两个串是唯一的合法解，此时 |a|+|b|=1 。

样例 3 显然是无解的，只是为了提醒一下大家记得判无解。

数据规模
对于 100% 的数据，1≤p<n≤50, m≤52n 。

- subtask1（30 分）：满足 n≤10, m≤20 。
- subtask2（10 分）：满足所有边权均为小写字母。
- subtask3（60 分）：满足 n≤50 。