现有一颗以1为根的树，节点编号从1到n.每条边有两个权值，分别为a和b.
输出n−1个数r2,r3 ⋯,rn，其中ri定义如下:
考虑从根节点(1号节点) 到第i号节点(2≤i≤n) 的路径，令沿该路径按权值a的花费为Ai，ri为该路径的最长前缀，使该前缀的权值b之和不大于Ai.

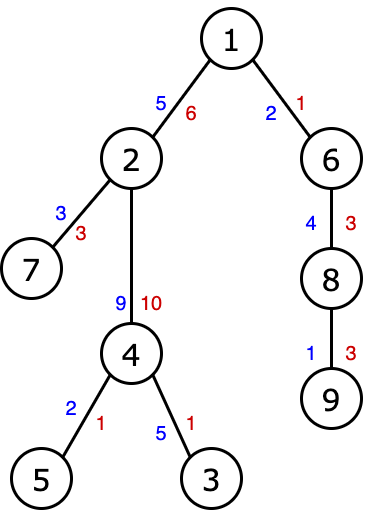
以n=9 时为例，如上图，蓝色数字表示a的花费，红色数字表示b的花费.
在这种情况下：
r2=0 ，因为到节点2的路径中有a=5，只有前缀为0时才可能有较小（或相等）的b；
r3=3 ， 因为到节点3的路径中a为5+9+5=19 ，长为3的前缀使b为6+10+1=17 (17≤19 符合题意 )；
r4=1 ， 因为到节点4的路径中a为5+9=14 ，长为1的前缀使b为6 (这是最长的符合题意的前缀， 因为长为 2的前缀b为6+10=16 ，大于14 )；
r5=2 ， 因为到节点5的路径中a为5+9+2=16 ，长为2的前缀使b为6+10=16 (这是最长的符合题意的前缀， 因为长为3的前缀的 b为6+10+1=17,比16 大)；
r6=1 ，因为到节点6的路径中a为2 ，长为1的前缀使b等于1；
r7=1 ，因为到节点7的路径中a为5+3=8，长为1的前缀使b等于6(这是最长的符合题意的前缀， 因为长为2的前缀的b为6+3=9 ，超出了期望的8 )；
r8=2，因为到节点8的路径中a为2+4=6，长为2的前缀使b为1+3=4；
r9=3，因为到节点9的路径中a为2+4+1=7 ，长为3的前缀使b为1+3+3=7.

第一行为整数T,表示有T (1≤T≤10000)组测试样例。
每组测试样例的第一行为整数n (2≤n≤200000)，表示顶点的数量。
接下来的n-1行，每行为3个整数pj,aj和bj(1≤pj≤n; 1≤aj,bj≤1e9),分别表示结点j的祖先pj、从pj至结点j的两个边权。
j的值从2到n. 输入数据保证生成的是一颗以1根的树，且所有n之和不超过200000.

每组测试样例，输出n-1个数：r2 r3 ...rn

4
9
1 5 6
4 5 1
2 9 10
4 2 1
1 2 1
2 3 3
6 4 3
8 1 3
4
1 1 100
2 1 1
3 101 1
4
1 100 1
2 1 1
3 1 101
10
1 1 4
2 3 5
2 5 1
3 4 3
3 1 5
5 3 5
5 2 1
1 3 2
6 2 1

0 3 1 2 1 1 2 3 
0 0 3 
1 2 2 
0 1 2 1 1 2 2 1 1 

测试样例2中。
r2=0, 因为到节点2的路径中有a=1，只有前缀为0时才可能有较小（或相等）的bj；
r3=0, 因为到节点3的路径中有a=1+1=2，只有前缀为1时b为100；
r4=3, 因为到节点4的路径中有a=1+1+101=103，前缀为3时b=102。