六一节快到了。
六一儿童图可以视为一个 n 个节点 m 条边的无向连通图,第 i 条边连接 u[i],v[i] 两个节点,权值为 w[i] 。
老师需要从六一儿童图上裁剪出一棵六一儿童树。
六一儿童树是六一儿童图上的一棵 n-1 条边的生成树,且树上所有边的边权值的最大值恰好等于 p 。
由于不一定能够成功从六一儿童图上裁剪出一棵六一儿童树,因此老师决定对树上的边权值进行修改,每次修改可以将任意一条边的边权值增加 1 或减少 1
求最少需要修改几次,才能使得老师能成功从六一儿童图上裁剪出一棵六一儿童树。
6567: 六一儿童树
时间限制: 2 Sec 内存限制: 512 MB提交: 4 解决: 3
[提交][状态][命题人:]
题目描述
输入
第一行包含一个整数 T (1≤T≤1000) ,表示数据组数。
每组数据第一行包含三个整数 n,m,p (2≤n≤2·10^5; n-1≤m≤min(2·10^5,n(n-1)/2); 1≤p≤10^9) ,分别表示节点数、边数、目标最大边权值。
每组数据接下来 m 行,第 i 行包含三个整数 u[i],v[i],w[i] ,表示第 i 条边连接 u[i],v[i] 两个节点,权值为 w[i] 。
保证输入的图是连通图,无重边。
保证所有数据的 n 之和与 m 之和均不超过 2·10^5 。
每组数据第一行包含三个整数 n,m,p (2≤n≤2·10^5; n-1≤m≤min(2·10^5,n(n-1)/2); 1≤p≤10^9) ,分别表示节点数、边数、目标最大边权值。
每组数据接下来 m 行,第 i 行包含三个整数 u[i],v[i],w[i] ,表示第 i 条边连接 u[i],v[i] 两个节点,权值为 w[i] 。
保证输入的图是连通图,无重边。
保证所有数据的 n 之和与 m 之和均不超过 2·10^5 。
输出
对于每组数据,输出一行包含一个整数,表示答案。
样例输入
Copy
4 4 5 7 4 1 3 1 2 5 2 3 8 2 4 1 3 4 4 4 6 5 1 2 1 1 3 1 1 4 2 2 4 1 4 3 1 3 2 1 3 2 10 1 2 8 1 3 10 5 5 15 1 2 17 3 1 15 2 3 10 1 4 14 2 5 8
样例输出
Copy
1 3 0 0
提示
样例解释
第一组数据如下所示:
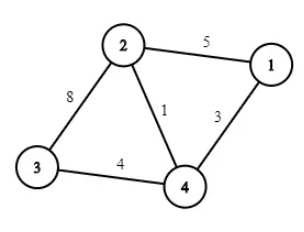
将 2-3 边的权值减少1 后,在得到如下的树:
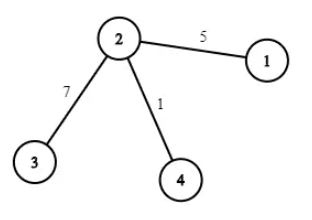
共操作 1 次。
第一组数据如下所示:

将 2-3 边的权值减少1 后,在得到如下的树:

共操作 1 次。